Engineering Mechanics - Analysis of Structures (II)

Analysis of Structures (II)

• Internal Forces(Beams)

Beams are structural members which offer resistance to bending due to applied loads. The cross- section of beams is much smaller compared to its length. Generally the largest dimension of the cross- section is less than 1/10th of the length. Loads are generally applied normal to the axes of the beams.

Types of Beam:

Beams supported such that their external support reactions can be calculated by the methods of statics alone are called statically determinate beams. A beam which has more supports than needed to provide equilibrium is statically indeterminate. To determine the support reactions for such a beam, compatibility of deformation is to be considered.

Three different types of statically determinate beams are shown in the next page. First is the simply supported beam. The left support can provide only vertical and horizonal reactions. The right support can provide only vertical reactions. Thus, there are three unknown reactions, which can be determined by the balancing vertical and horizontal forces and a moment.

The second beam is a cantilevered beam. Here, the beam is fixed at one end and free at the other end. Fixed support offers vertical and horizontal reactions as well as a moment.

The third beam is an over hanged beam, similar to simply supported beam. Only difference is that right support is not at the end.

• Differential Equilibrium Equation

In the last lecture, for finding out the internal force and moments, beams were cut into 2 parts. In this lecture, an alternative procedure is suggested. Instead of cutting a beam in two and applying the equilibriums conditions to one of the segments we consider a very small element of the beam as a free body. From the force balance, differential equations can be obtained. Solution of differential equations will provide shear fore and bending moment.

Consider the beam as shown below:

Cutting a small element at a distance x , we obtain the following free body diagram , which is shown next.

• Cables

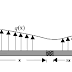
Flexible cables are used in suspension bridges, transmission lines, messenger cables, for supporting heavy trolley and lift, as telephone lines, and many other applications. In suspension bridges the cables supports a large load. The weigth of the cable itself in such cases may be considered negligible. In trabsmission lines, on the other hand, the principal force is the weight of the cable itself.

Assumptions:

(1) Cable is perfectly flexible. It can't take any bending or compressive load. At the centre of the cross section of the cable only a tensile force is transmitted and there can be no bending moment there. Therefore, the force transmitted through the cable must be tangent to the cable at all position, along the cable.

(2) Cable is perfectly inextensible. This means that the length of the cable is constant.

Consider the case of a cable suspended between two rigid supports A and B under the action of a loading function w(x) given per unit length measured in the horizontal direction. The loading will be considered coplaner with the cable and directed vertically. Consider an element of the cable of length Δs as a free body.