Geometry Dependent Properties

• Centre of Mass & Centre of Gravity

Consider a uniform rod of length L. When the rod is placed horizontally, each particle of the rod is pulled by the gravitional force of the earth. The sum of all three forces will be equal to the total weight of the rod.

Consider two systems: One is the rod AB of weight W and other is a concentrated weight W, at a distance 1/3 L from point A.

These two systems are equivalent as far as the net gravitational pull is concerned, but the moment of the gravitational forces of the two systems about point A is different.

• Second Moments and the product of area of a plane

The second moments of the area A about the x and y axes denoted as I_xx and I_yy , respectively are defined as:

Note that, 

(1) The first moment of area can be positive or negative, whereas the second moment of area is positive only.

(2) The element of area that are farthest from the axis contribute most to the second moment of area.

Introduction to Friction

• Friction

Friction is the force distribution at the surface of contact between two bodies that prevents or impedes sliding motion of one body relative to the other. This force distribution is tangent to the contact surface and has, for the body under consideration, a direction at every point in the contact surface that is in opposition to the possible or existing slipping motion of the body at that point.

A force is applied to body sliding on the floor. After sometime, the force is removed, but the body keeps moving, since it has already attained the velocity. However, after some time the body comes to rest. It is the frictional force, which causes body to stop. If the frictional force were not there, body would have kept moving.

• Application of Friction

In this lecture, few applications of friction are presented.

Wedges

Wedges are small pieces of material with two of its opposite surfaces not parallel. They are used to lift heavy blocks, machinery, precast beam etc., slightly, required for final alignment or to make place for inserting lifting devices. The weight of the wedge is very small compared to the weight lifted. Hence, in all the problems, weight of wedges may be negleted. The following figure is showing a wedge:

Engineering Mechanics - Analysis of Structures (II)

Analysis of Structures (II)

• Internal Forces(Beams)

Beams are structural members which offer resistance to bending due to applied loads. The cross- section of beams is much smaller compared to its length. Generally the largest dimension of the cross- section is less than 1/10th of the length. Loads are generally applied normal to the axes of the beams.

Types of Beam:

Beams supported such that their external support reactions can be calculated by the methods of statics alone are called statically determinate beams. A beam which has more supports than needed to provide equilibrium is statically indeterminate. To determine the support reactions for such a beam, compatibility of deformation is to be considered.

Three different types of statically determinate beams are shown in the next page. First is the simply supported beam. The left support can provide only vertical and horizonal reactions. The right support can provide only vertical reactions. Thus, there are three unknown reactions, which can be determined by the balancing vertical and horizontal forces and a moment.

The second beam is a cantilevered beam. Here, the beam is fixed at one end and free at the other end. Fixed support offers vertical and horizontal reactions as well as a moment.

The third beam is an over hanged beam, similar to simply supported beam. Only difference is that right support is not at the end.

• Differential Equilibrium Equation

In the last lecture, for finding out the internal force and moments, beams were cut into 2 parts. In this lecture, an alternative procedure is suggested. Instead of cutting a beam in two and applying the equilibriums conditions to one of the segments we consider a very small element of the beam as a free body. From the force balance, differential equations can be obtained. Solution of differential equations will provide shear fore and bending moment.

Consider the beam as shown below:

Cutting a small element at a distance x , we obtain the following free body diagram , which is shown next.

• Cables

Flexible cables are used in suspension bridges, transmission lines, messenger cables, for supporting heavy trolley and lift, as telephone lines, and many other applications. In suspension bridges the cables supports a large load. The weigth of the cable itself in such cases may be considered negligible. In trabsmission lines, on the other hand, the principal force is the weight of the cable itself.

Assumptions:

(1) Cable is perfectly flexible. It can't take any bending or compressive load. At the centre of the cross section of the cable only a tensile force is transmitted and there can be no bending moment there. Therefore, the force transmitted through the cable must be tangent to the cable at all position, along the cable.

(2) Cable is perfectly inextensible. This means that the length of the cable is constant.

Consider the case of a cable suspended between two rigid supports A and B under the action of a loading function w(x) given per unit length measured in the horizontal direction. The loading will be considered coplaner with the cable and directed vertically. Consider an element of the cable of length Δs as a free body.

Engineering Mechanics - Analysis of Structures (I)

Analysis of Structures (I)

• Trusses

A framework composed of members joined at their ends to form a structure is called a truss. Truss is used for supporting moving or stationary load. Bridges, roof supports, derricks, and other such structures are common example of trusses. When the members of the truss lie essentially in a single plane, the truss is called a plane truss.

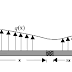
Fig. 3.1 shows most basic triangular truss. Members are connected by pin-joints, which arrest translation but not rotation. Each member has three degrees of freedom in a plane, two translations and one rotation. Total degrees of freedom are 9. Each pin joint arrests two degree of freedom. Hence, degrees of freedom of pin-joint connected structure is 3. For keeping the structure stationary, these three degrees of freedom should be arrested. In the figure, left fixed support arrests two degrees of freedom, whereas in the right, the roller support arrests one degree of freedom. Thus the structure cannot move and the structure is called stable. This type of structure is also called rigid structure.

• 

Fig 3.1: A 3-member truss

• Frames

A structure is called a frame if at least one of its individual members is a multiforce member. A multiforce member is defined as one with three or more forces acting on it, or one with two or more forces and one or more couples acting on it. Frames are structures which are designed to support applied loads and are usually fixed in position.

Frames:

1. Support loads.

2. Usually stationary.

3. Fully constrained.

Not all forces are directed along the members as in a truss. In a member of truss, forces are directed along the member only. For example, in the following illustration, truss is subjected to compressive forces.

• Machines

Frames and machines are built-up structural and mechanical systems consisting of multiple parts assembled together in a number of possible ways. For example, the parts could be pin-connected or welded together. The primary difference between frames and machines is that there are moving parts in machines and not in frames. The method of analysis is the same. Although machines involve moving parts, we analyze the system at one instant in time when the positions of individual parts and the applied loads are clearly defined. The solution to these systems usually requires the drawing of the free-body diagrams of individual parts, and the application of the equilibrium equations.

When a frame or machine is broken up into multiple parts, the forces and/or moments present at the points of separation must be shown on the free-body diagrams of the separated parts in a manner consistent with the third law of Newton. That is the forces and moments are shown as equal and opposite on the two parts that have been separated.

Some important definitions

Load: This is the resistance to be overcome by the machine.

Effort : This is the force required to overcome the resistance to get the work done by the machine.

Mechanical advantage: This is the ratio of load lifted to effort applied. Thus, if W is the load and P is the corresponding effort, then

Mechanical Advantage = 

Engineering Mechanics - Basics of Statics

Basics of Statics

• Fundamentals of Mechanics

Imagine the following situations:

(a) You have to design a car, which can run at a speed of 140 km/hr on an expressway. In order to do this, you have to find engine power and the forces acting on the car body. Forces will come due to wind resistance, rolling resistance and inertia.

(b)You want to find out the power needed for a CD driver motor.

(c)A nozzle issues a jet of water with a high velocity, which impinges upon the blades of turbine. The blades deflect the jet of water through an angle. You have to find out the force exerted by the jet upon the turbine.

• Equation of Equilibrium

A particle is in equilibrium if it is stationary or it moves uniformly relative to an inertial frame of reference. A body is in equilibrium if all the particles that may be considered to comprise the body are in equilibrium.

One can study the equilibrium of a part of the body by isolating the part for analysis. Such a body is called a free body. We make a free body diagram and show all the forces from the surrounding that act on the body. Such a diagram is called a free-body diagram. For example, consider a ladder resting against a smooth wall and floor. The free body diagram of ladder is shown in the right.

Three forces are acting on the ladder. Gravitational pull of the earth (weight), W of the ladder, reaction of the floor R₂ and reaction of the wall R₁ .